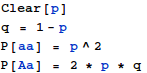
The Red-Haired Girl named Florida
In The Drunkard’s Walk, Leonard Mlodinow presents The Girl Named Florida Problem:“In a family with two children, what are the chances, if [at least] one of the children is a girl named Florida, that both children are girls?”
I like this problem, and I use it on the first day of my class to introduce the topic of conditional probability. But I’ve decided that it’s too easy. To give it a little more punch, I’ve decided to combine it with the Red-Haired Problem to get this:
In a family with two children, what are the chances, if at least one of the children is a girl with red hair, that both children are girls?
You can make some simplifying assumptions: About 2% of the world population has red hair. Assume that the alleles for red hair are purely recessive, and there is no mutation. Also, assume that the Red Hair Extinction theory is false, so you can apply the Hardy–Weinberg principle. Finally, you can ignore the effect of identical twins.
As before, I’ll define p to be the prevalence of red-hair alleles, so q=1-p is the prevalence of other alleles. P[aa] is the prevalence of red hair, and P[Aa] is the prevalence of heterozygous red hair “carriers.”
In[43]:=
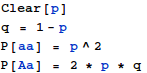
Out[44]=
![]()
Out[45]=
![]()
Out[46]=
![]()
If a couple has at least one red haired child, both of them must have a red hair allele to contribute, so the only possible combinations are Aa Aa, Aa aa, and aa aa. The prior probabilities for these combinations are:
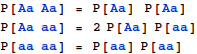
Out[50]=
![]()
Out[51]=
![]()
Out[52]=
![]()
For each possible combination, we can compute the likelihood of the evidence --- at least one red haired girl --- and use those likelihoods to compute the posterior probabilities (nc is the normalizing constant):
In[101]:=

Out[101]=
![]()
Out[102]=
![]()
Out[103]=
![]()
Out[104]=
![]()
And for each possible combination, we can apply the “girl named Florida” formula to get the probability of two girls (GG). Finally, we apply the law of total probability to get P[GG | E]:
In[89]:=
![]()
Out[89]=
![]()
We can express P[GG | E] as a function of p, and then evaluate it at P[aa] = p^2 = 0.02 :
In[95]:=
![]()
Out[95]=
![]()
Out[96]=
![]()
So the final answer is 45.6%. More generally, here’s what that looks like for p in the range [0, 1]:
In[92]:=
![]()
Out[92]=

When p=1, everyone has red hair, so the red-haired information is redundant and the question reduces to P[GG | at least one girl], which is 1/3.
If p=0, the likelihood of the evidence is 0 under all hypotheses, so the answer is undefined. But as p approaches zero, the prevalence of Aa Aa dominates the other possible combinations, so the answer approaches 7/15.