This HTML version of Think Perl 6 is provided for convenience, but it is not the best format of the book. You might prefer to read the PDF version.
Chapter 4 Loops, Conditionals, and Recursion
The main topic of this chapter is the if statement, which executes different code depending on the state of the program. But first I want to introduce two new operators: integer division and modulo.
4.1 Integer Division and Modulo
The integer division operator, div, divides
two numbers and rounds down to an integer. For example,
suppose the
run time of a movie is 105 minutes. You might want to know how
long that is in hours. In Perl, conventional division
returns a rational number (in many languages, it returns a
floating-point number, which is another kind of internal
representation for noninteger numbers):
> my $minutes = 105; > $minutes / 60; 1.75
But we don’t normally write hours with decimal points. Integer division returns the integer number of hours, dropping the fraction part:
> my $minutes = 105; > my $hours = $minutes div 60; 1
In arithmetic, integer division is sometimes called Euclidean division, which computes a quotient and a remainder.
To get the remainder, you could subtract off one hour in minutes:
> my $remainder = $minutes - $hours * 60; 45
An alternative is to use the modulo operator, %, which
divides two numbers and returns the remainder:
> my $remainder = minutes % 60; 45
The modulo operator is very common in programming languages and is more useful than it seems. For example, you can check whether one number is divisible by another—if $dividend % $divisor is zero, then $dividend is divisible by $divisor. This is commonly used, for example, with a divisor equal to 2 in order to determine whether an integer is even or odd. We will see an example of that later in this chapter (see Section ??).
To tell the truth, Perl 6 also has a specific operator for
divisibility, %%. The $dividend %% $divisor
expression returns a true value if
$dividend % $divisor is equal to 0,
that is if $dividend is divisible by $divisor (and false otherwise):
> 42 %% 2; True
Also, you can extract the rightmost digit or digits from a number with the modulo operator. For example, $x % 10 yields the rightmost digit of $x (in base 10). Similarly, $x % 100 yields the last two digits:
> 642 % 100; 42
4.2 Boolean Expressions
A Boolean expression is an expression that is either true or false. The following examples use the operator ==, which compares two numeric operands and produces True if they are equal and False otherwise:
> 5 == 5; True > 5 == 6; False
True and False are special values that belong to the type Bool; they are not strings:
> say True.WHAT (Bool) > say False.WHAT (Bool)
The == operator is one of the numeric relational operators and checks whether the operands are equal; the others are:
$x != $y # $x is not numerically equal to $y
$x > $y # $x is numerically greater than $y
$x < $y # $x is numerically less than $y
$x >= $y # $x is numerically greater than or equal to $y
$x <= $y # $x is numerically less than or equal to $y
$x === $y # $x and $y are truly identical
Although these operations are probably familiar to you, the Perl symbols are different from the mathematical symbols. A common error is to use a single equals sign (=) instead of a double equals sign (==). Remember that = is an assignment operator and == is a relational operator. There is no such thing as =<, and there exists a => operator, but it is not a relational operator, but something completely different (it is, as we’ll see later, a pair constructor).
The difference between == and === is that the former operator checks whether the values of the operands are equal and the latter checks whether the operands are truly identical. As an example, consider this:
say 42 == 42; # True say 42 == 42.0; # True say 42 === 42; # True say 42 === 42.0; # False
These relational operators can only compare numeric values (numbers or variables containing numbers) or values that can be coerced to numeric values, such as, for example, the string "42" which, if used with these operators (except ===), will be coerced to the number 42.
For comparing strings (in a lexicographic or “pseudo- alphabetic” type of comparison), you need to use the string relational operators:
$x eq $y # $x is string-wise equal to $y
$x ne $y # $x is string-wise not equal to $y
$x gt $y # $x is greater than $y (alphabetically after)
$x lt $y # $x is less than $y (alphabetically before)
$x ge $y # $x is greater than or equal to $y
$x le $y # $x is less than or equal to $y
$x eqv $y # $x is truly equivalent to $y
For example, you may compare (alphabetically) two former US presidents:
> 'FDR' eq 'JFK'; False > 'FDR' lt 'JFK'; # alphabetical comparison True
Unlike most other programming languages, Perl 6 allows you to chain relational operators transitively, just as in mathematical notation:
say 4 < 7 < 12; # True say 4 < 7 < 5; # False
It may be useful to point out that numeric relational operators and string relational operators don’t work the same way (and that’s a good reason for having different operators), because they don’t have the same idea of what is greater than or less than.
When comparing two positive integers, a number with four digits is always greater than a number with only two or three digits. For example, 1110 is greater than 886.
String comparisons, in contrast, basically follow (pseudo) alphabetical rules: “b” is greater than “aaa”, because the commonly accepted rule for string comparisons is to start by comparing the first letter of each string: which string is greater is known if the two letters are different, irrespective of what character comes next; you need to proceed to comparing the second letter of each word only if comparing the first letter of each string led to a draw, and so on. Thus, any word starting with “a” is less than any word starting with “b”, irrespective of the length of these words. You may think that this is nitpicking, but this becomes essential when you start sorting items: you really have to think about which type of order (numeric or alphabetical) you want to use.
There are also some so-called “three-way” relational operators,
cmp, <=> and leg, but we’ll come back to them
when we study how to sort the items of a list. Similarly, we need
to learn quite a few other things about Perl before we can do
justice to the incredibly powerful and expressive smart match
operator, ~~.
A final point to be noted about string comparisons is that uppercase letters are always deemed smaller than lowercase letters. So "A," "B," "BB," and "C" are all less than "a," "b," "bb," and "c." We will not go into the details here, but this becomes more complicated (and sometimes confusing) when the strings to be compared contain nonalphabetical characters (or non-ASCII Unicode letters).
4.3 Logical Operators
There are three main pairs of logical operators:
- logical and: “and” and &&
- logical or: “or” and ||
- logical not: “not” and !
The semantics (meaning) of these operators is similar to their meaning in English. For example, $x > 0 and $x < 10 is true only if $x is greater than 0 and less than 10.
$n % 2 == 0 and $n % 3 == 0 is true if both conditions are true, that is, if the number is divisible by 2 and by 3, i.e., is in fact divisible by 6 (which could be better written as: $n % 6 == 0 or $n %% 6).
$n % 2 == 0 or $n % 3 == 0 is true if either or both of the conditions is true, that is, if the number is divisible by 2 or by 3 (or both).
Finally, the not operator negates a Boolean expression, so not (x > y) is true if x > y is false, that is, if x is less than or equal to y.
The &&, ||, and ! operators have the same meanings, respectively, as and, or, and not, but they have a tighter precedence, which means that when they stand in an expression with some other operators, they have a higher priority of execution. We will come back to precedence later, but let’s say for the time being that, in most common cases, the and, or, and not operators will usually do what you want.
Strictly speaking, the operands of the logical operators should be Boolean expressions, but Perl, just like many languages partly derived from C, is not very strict on that. The numbers 0 and 0.0 are false; and any nonzero number or nonempty string is interpreted as True:
> 42 and True; True
This flexibility can be very useful, but there are some subtleties to it that might be confusing. You might want to avoid it unless you know what you are doing.
The so built-in function returns a Boolean evaluation of its argument:
> say so (0 and True); False
Here, the expression (0 and True) is false because 0 is false and the expression could be true only if both arguments of the and operator were true.
When several Boolean conditions are linked with some logical operator, Perl will only perform the comparisons that are strictly necessary to figure out the final result, starting with those on the left. For example, if you write:
> False and $number > 0; False
there is no need to evaluate the second Boolean expression to know that the overall expression will be false. In this case, Perl does not try to check whether the number is positive or even whether it is defined. It is sometimes said that these operators “short circuit” unnecessary conditions.
Similarly, in the following code, the compute-pension subroutine will not even be called if the person’s age is less than 65:
$age >= 65 and compute-pension();
The same goes with the or operator, but the other way around: if the first boolean expression of an or statement is true, then the next expression will not be evaluated. The following code is thus equivalent to the previous one:
$age < 65 or compute-pension();
This can be a way of running the compute-pension subroutine conditionally, depending on the value of the age, and this is sometimes used, notably in idiomatic constructs such as:
do-something() or die "could not do something";
which aborts the program if do-something returns a false value, meaning that it was not able to do something so essential that it would not make sense to try to continue running it.
We will examine now clearer and much more common ways of running conditional code.
4.4 Conditional Execution
In order to write useful programs, we almost always need the ability to check conditions and change the behavior of the program accordingly. Conditional statements give us this ability. The simplest form is the if statement:
if $number > 0 {
say '$number is positive';
}
The Boolean expression after if is called the condition. If it is true, the subsequent block of code runs. If not, nothing happens. The block of code may contain any number of statements.
It is conventional and highly recommended (although not strictly mandatory from the standpoint of the compiler) to indent the statements in the block, in order to help visualize the control flow of the program, i.e., its structure of execution: with such indentation, we can see much better that the statements within the conditional block will run only if the condition is true.
The condition may be a compound Boolean expression:
if $n > 0 and $n < 20 and $n %% 2 {
say '$n is an even and positive number smaller than 20'
}
Note that in the print statement above, the final semi-colon has been omitted. When a statement is the last code line of a block, immediately before the curly brace } closing that code block, the final semi-colon is optional and may be omitted, though it might be considered good form to include it.
In theory, the overall code snippet above is itself a statement and should also end with a semi-colon after the closing brace. But a closing curly brace followed by a newline character implies a statement separator, so you don’t need a semi-colon here and it is generally omitted.
4.5 Alternative Execution
A second form of the if statement is “alternative execution,”
in which there are two possibilities and the condition determines
which one runs. Given a $number variable containing an
integer, the following code displays two different messages
depending on whether the value of the integer is even or odd::
if $number % 2 == 0 {
say 'Variable $number is even'
} else {
say 'Variable $number is odd'
}
If the remainder when $number is divided by 2 is 0, then we know that $number is even, and the program displays an appropriate message. If the condition is false, the second set of statements runs. Since the condition must be true or false, exactly one of the alternatives will run. The alternatives are called branches, because they are branches in the flow of execution.
Note that if $number is evenly divisible by two,
this code will print:
Variable $number is even
The $number variable value is not interpolated,
because we used single quotes for the purpose
of printing out the variable name rather
than its value. We would have to use double quotes if
we wanted to display the variable’s value instead of its
name.
4.6 Chained Conditionals
Sometimes there are more than two possibilities and we need more than two branches. One way to express a computation like that is a chained conditional:
if $x < $y {
say 'Variable $x is less than variable $y'
} elsif $x > $y {
say 'Variable $x is greater than variable $y'
} else {
say 'Variables $x and $y are equal'
}
The elsif keyword is an abbreviation of “else if” that has the advantage of avoiding nesting of blocks. Again, exactly one branch will run. There is no limit on the number of elsif statements.
If there is an else clause, it has to be at the end, but there doesn’t have to be one:
if $choice eq 'a' {
draw_a()
} elsif $choice eq 'b' {
draw_b()
} elsif $choice eq 'c' {
draw_c()
}
Each condition is checked in order. If the first is false, the next is checked, and so on. If one of them is true, the corresponding branch runs and the statement ends. Even if more than one condition is true, only the first true branch runs.
4.7 Nested Conditionals
One conditional can also be nested within another. We could have written the example in the previous section like this:
if $x == $y {
say 'Variables $x and $y are equal'
} else {
if $x < $y {
say 'Variable $x is less than variable $y'
} else {
say 'Variable $x is greater than variable $y'
}
}
The outer conditional contains two branches. The
first branch contains a simple statement. The second branch
contains another if statement, which has two branches of its
own. Those two branches are both simple statements,
although they could have been conditional statements as well.
The if $x < $y conditional is said to be nested within
the else branch of the outer conditional.
Such nested conditionals show how critical it is for your own comprehension to properly indent conditional statements, as it would be very difficult here to visually grasp the structure without the help of correct indentation.
Although the indentation of
the statements helps make the structure apparent,
nested conditionals become difficult to read very
quickly. It is a good idea to avoid them when you can.
Logical operators often provide a way to simplify nested
conditional statements. For example, consider the
following code (which assumes $x to be an integer):
my Int $x;
# ... $x = ...;
if 0 < $x {
if $x < 10 {
say 'Value of $x is a positive single-digit number.'
}
}
The say statement runs only if we make it past both conditionals, so we can get the same effect with the and Boolean operator, and the code can be rewritten using a single conditional:
if 0 < $x and $x < 10 {
say '$x is a positive single-digit number.'
}
For this kind of condition, Perl 6 provides a more concise option using the chained relational operators described earlier:
if 0 < $x < 10 {
say '$x is a positive single-digit number.'
}
4.8 If Conditionals as Statement Modifiers
There is also a form of if called a statement modifier (or sometimes “postfix conditional”) form when there is only one conditional statement. In this case, the if and the condition come after the code you want to run conditionally. Note that the condition is still always evaluated first:
say '$number is negative.' if $number < 0;
This is equivalent to:
if $number < 0 {
say '$number is negative.'
}
This syntactic form is more concise as it takes only one code line instead of three. The advantage is that you can see more of your program code on one screen, without having to scroll up and down. However, this syntax is neat and clean only when both the condition and the statement are short and simple, so it is probably best used only in these cases.
The statement modifier form does not allow else and elsif statements.
4.9 Unless Conditional Statement
If you don’t like having to write negative conditions in a conditional if statement such as:
if not $number >= 0 {
say '$number is negative.'
}
you may write this instead:
unless $number >= 0 {
say '$number is negative.'
}
This unless keyword does exactly what the English says:
it will display the sentence “$number is negative.”
unless the number is greater than or equal to 0.
You cannot use else or elsif statements with unless, because that would end up getting confusing.
The unless conditional is most commonly used in its statement modifier (or postfix notation) form:
say '$number is negative.' unless $number >= 0;
4.10 For Loops
Suppose you need to compute and print the product of the first five positive digits (1 to 5). This product is known in mathematics as the factorial of 5 and is sometimes written as 5!. You could write this program:
my $product = 1 * 2 * 3 * 4 * 5; say $product; # prints 120
You could make it slightly simpler:
say 2 * 3 * 4 * 5; # prints 120
The problem is that this syntactic construct does not scale well and becomes tedious for the product of the first ten integers (or factorial 10). And it becomes almost a nightmare for factorial 100. Calculating the factorial of a number is a fairly common computation in mathematics (especially in the fields of combinatorics and probability) and in computer science. We need to automatize it, and using a for loop is one of the most obvious ways of doing that:
my $product = 1;
for 1..5 {
$product *= $_
}
say $product; # prints 120
Now, if you need to compute factorial 100, you just need to replace the 5 in the code above with 100. Beware, though, the factorial function is known to grow extremely rapidly, and you’ll get a truly huge number, with 158 digits (i.e., a number much larger than the estimated total number of atoms in the known universe).
In this script, 1..5 is the range operator, which is used here
to generate a list of consecutive numbers between 1 and 5. The
for keyword is used to iterate over that list, and
$_ is a special variable that takes each successive
value of this list: first 1, then 2, etc. until 5. In the code
block forming the body of the loop, the $product variable
is multiplied successively by each value of $_. The loop
ends with 5 and the result, 120, is printed on the last line.
This is a simple use of the for statement, but probably not the most commonly used in Perl 6; we will see more below. We will also see other types of loops. But that should be enough for now to let you write some loops. Loops are found everywhere in computer programming.
The $_ special variable is known as the topical
variable or simply the topic. It does not need to be declared
and many syntactic constructs assign a value to it without
explicitly mentioning it. Also, $_ is a implicit argument
to methods called without an explicit invocant. For example,
to print the first five integers, you might write:
for 1..5 {.say}; # prints numbers 1 to 5, each on its line
Here .say is a syntax shorthand equivalent to $_.say.
And since, as we saw, $_ takes each successive value of
the range introduced by the for keyword, this very short code
line prints each number between 1 and 5, each on a different line.
This is a typical example of the $_ topical variable being used
without even being explicitly mentioned. We will see many other
uses of the $_ special variable.
Sometimes, you don’t use the $_ loop variable within the
loop, for example if you just want to do something five times but don’t
care each time through the loop at which iteration you
have arrived. A subroutine that prints a message n times
might look like this:
sub print-n-times (Int $n, Str $message) {
for 1..$n { say $message }
}
The for loop also has a statement modifier or postfix form, used here to compute again the factorial of 5:
my $product = 1; $product *= $_ for 1..5; say $product; # prints 120
There is another syntax for the for loop, using an explicit loop variable:
sub factorial (Int $num) {
my $product = 1;
for 1..$num -> $x {
$product *= $x
}
return $product
}
say factorial 10; # 3628800
The for loop in this subroutine is using what is called
a “pointy block” syntax. It is essentially the same idea
as the previous for loops, except that,
instead of using the $_ topical variable, we
now declare an explicit $x loop variable with the
1..$num -> $x syntax to iterate over the range
of values. Using an explicit loop variable can make your
code clearer when things get more complicated, for example
when you need to nest several for loops. We will
see more examples of that later.
We will also see several other ways of computing the factorial of a number in this book.
4.11 Recursion
It is legal for one function or subroutine to call another; it is also legal for a subroutine to call itself. It may not be obvious why that is a good thing, but it turns out to be one of the most magical things a program can do. For example, look at the following subroutine:
sub countdown(Int $time-left) {
if $time-left <= 0 {
say 'Blastoff!';
} else {
say $time-left;
countdown($time-left - 1);
}
}
If $n is 0 or negative, it outputs the word, “Blastoff!”. Otherwise, it outputs the value of $time-left and then calls a subroutine named countdown—itself—passing $n-1 as an argument.
What happens if we call the subroutine like this?
countdown(3);
The execution of countdown begins with $time-left = 3, and since $time-left is greater than 0, it outputs the value 3, and then calls itself...
The execution of countdown begins with $time-left = 2, and since $time-left is greater than 0, it outputs the value 2, and then calls itself...The execution of countdown begins with $time-left = 1, and since $time-left is greater than 0, it outputs the value 1, and then calls itself...The execution of countdown begins with $time-left = 0, and since $time-left is not greater than 0, it outputs the word, “Blastoff!” and then returns.The countdown that got $time-left = 1 returns.
The countdown that got $time-left = 2 returns.
The countdown that got $time-left = 3 returns.
And then you’re back in the main program. So, the total output looks like this:
3 2 1 Blastoff!
A subroutine that calls itself is recursive; the process of executing it is called recursion.
As another example, we can write a subroutine that prints a string $n times:
sub print-n-times(Str $sentence, Int $n) {
return if $n <= 0;
say $sentence;
print-n-times($sentence, $n - 1);
}
If $n <= 0, the return statement exits the subroutine. The flow of execution immediately returns to the caller, and the remaining lines of the subroutine don’t run. This illustrates a feature of the return statement that we have not seen before: it is used here for flow control, i.e., to stop the execution of the subroutine and pass control back to the caller. Note also that, here, the return statement does not return any value to the caller; print-n-times is a void function.
The rest of the subroutine is similar to countdown: it displays $sentence and then calls itself to display $sentence $n − 1 additional times. So the number of lines of output is 1 + ($n - 1), which adds up to $n.
For simple examples like this, it may seem easier to use a for loop. But we will see examples later that are hard to write with a for loop and easy to write with recursion, so it is good to start early.
4.12 Stack Diagrams for Recursive Subroutines
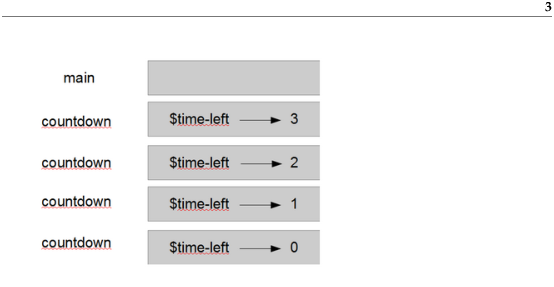
In Section ??, we used a stack diagram to represent the state of a program during a subroutine call. The same kind of diagram can help interpret a recursive subroutine.
Every time a subroutine gets called, Perl creates a frame to contain the subroutine’s local variables and parameters. For a recursive subroutine, there might be more than one frame on the stack at the same time.
Figure ?? shows a stack diagram for countdown called with n = 3.
Figure 4.1: Stack diagram.
As usual, the top of the stack is the frame for the main program. It is empty because we did not create any variables in it or pass any arguments to it.
The four countdown frames have different values for the parameter $time-left. The bottom of the stack, where $time-left = 0, is called the base case. It does not make a recursive call, so there are no more frames.
As an exercise, draw a stack diagram for print-n-times
called with
$sentence = 'Hello' and $n = 2.
Then write a function called do-n-times that takes a function
and a number, $num, as arguments, and that calls
the given function $num times.
Solution: see Section ??
4.13 Infinite Recursion
If a recursion never reaches a base case, it goes on making recursive calls forever, and the program never terminates. This is known as infinite recursion, and it is generally not a good idea. In fact, your program will not actually execute forever but will die at some point when the computer runs out of memory or some other critical resource.
You have to be careful when writing recursive subroutines. Make sure that you have a base case, and make sure that you are guaranteed to reach it. Actually, although this is not absolutely required by the language, I would advise you to take the good habit of treating the base case first.
4.14 Keyboard Input
The programs we have written so far accept no input from the user. They just do the same thing every time. Perl provides built-in functions that stop the program and wait for the user to type something.
For example, the prompt function prompts the user with
a question or an instruction. When the user presses
Return or Enter, the program resumes and
prompt returns what the user typed as a string
(without the newline character corresponding to the
Return key typed by the user):
my $user = prompt "Please type in your name: "; say "Hello $user";
This is probably one of the most common ways to obtain interactive user input, because it is usually a good idea to tell the user what is expected.
Another possibility is to use the get method (which reads a single line) on standard input:
say "Please type in your name: "; my $user = $*IN.get; say "Hello $user";
or the get function, which reads a line from standard input by default:
say "Please type in your name: "; my $user = get; say "Hello $user";
4.15 Program Arguments and the MAIN Subroutine
There is another (and often better) way to have a program use varying input defined by the user, which is to pass command-line arguments to the program, just as we have passed arguments to our subroutines.
The easiest way to retrieve arguments passed to a program is
to use a special subroutine named MAIN. A program that
has a defined MAIN subroutine will usually start its execution
with that subroutine and the command-line arguments supplied
to the program will be passed as arguments to MAIN.
The MAIN signature will enable you to
retrieve the arguments provided in the command line and
possibly also check their validity.
For example, the greet.pl6 program might look like this:
sub MAIN (Str $name) {
say "Hello $name";
}
You may call this program twice with different command-line arguments as follows:
$ perl6 greet.pl6 Larry Hello Larry $ perl6 greet.pl6 world Hello world
It is very easy to change the argument, since all you need to do at the operating system command line is use the up arrow and edit the end of the previous command line.
If you forget to supply the argument (or provide the wrong number of arguments, or arguments not matching the signature), the program will die and Perl 6 will nicely generate and display a usage method:
$ perl6 greet.pl6 Usage: greet.pl6 <name>
4.16 Debugging
When a syntax or runtime error occurs, the error message contains a lot of information, but it can be overwhelming. The most useful parts are usually:
- What kind of error it was
- Where it occurred
Syntax errors are usually easy to find, but there are a few gotchas. In general, error messages indicate where the problem was discovered, but the actual error might be earlier in the code, sometimes on a previous line or even many lines before.
For example, the goal of the following code was to display the multiplication tables:
# WARNING: faulty code
sub multiplication-tables {
for 1..10 -> $x {
for 1..10 -> $y {
say "$x x $y\t= ", $x * $y;
say "";
}
}
multiplication-tables();
It failed at compilation with the following error:
$ perl6 mult_table.pl6 ===SORRY!=== Error while compiling /home/Laurent/mult_table.pl6 Missing block (taken by some undeclared routine?) at /home/Laurent/mult_table.pl6:9 ------> multiplication-tables();<HERE><EOL>
The error message reports an error on line 9 of the program (the last line of the code), at the end of the line, but the actual error is a missing closing brace after line 4 and before line 5. The reason for this is that, while the programmer made the mistake on line 4, the Perl interpreter could not detect this error before it reached the end of the program. The correct program for displaying multiplication tables might be:
sub multiplication-tables {
for 1..10 -> $x {
for 1..10 -> $y {
say "$x x $y\t= ", $x * $y;
}
say "";
}
}
multiplication-tables();
When an error is reported on the last line of a program, it is quite commonly due to a missing closing parenthesis, bracket, brace, or quotation mark several lines earlier. An editor with syntax highlighting can sometimes help you.
The same is true of runtime errors. Consider this program aimed at computing 360 degrees divided successively by the integers between 2 and 5:
# WARNING: faulty code my ($a, $b, $c, $d) = 2, 3, 5; my $value = 360; $value /= $_ for $a, $b, $c, $d; say $value;
This programs compiles correctly but displays a warning and then an exception on runtime:
Use of uninitialized value of type Any in numeric context in block at product.pl6 line 3 Attempt to divide 12 by zero using div in block <unit> at product.pl6 line 4
The error message indicates a “division by zero” exception on line 4, but there is nothing wrong with that line. The warning on line 3 might give us a clue that the script attempts to use an undefined value, but the real error is on the first line of the script, where one of the four necessary integers (4) was omitted by mistake from the list assignment.
You should take the time to read error messages carefully, but don’t assume they point to the root cause of the exception; they often point to subsequent problems.
4.17 Glossary
- Integer division
- An operation, denoted div, that divides two numbers and rounds down (toward zero) the result to an integer.
- Modulo operator
- An operator, denoted with a percent sign (%), that works on integers and returns the remainder when one number is divided by another.
- Boolean expression
- An expression whose value is either True or False.
- Relational operator
- One of the operators that compares its operands. The most common numeric relational operators are ==, !=, >, <, >=, and <=. The equivalent string relational operators are eq, ne, gt, lt, ge, and le.
- Logical operator
- One of the operators that combines Boolean expressions: and, or, and not. The equivalent higher-precedence operators are &&, ||, and !
- Conditional statement
- A statement that controls the flow of execution depending on some condition.
- Condition
- The boolean expression in a conditional statement that determines which branch runs.
- Branch
- One of the alternative sequences of statements in a conditional statement.
- Chained conditional
- A conditional statement with a series of alternative branches.
- Nested conditional
- A conditional statement that appears in one of the branches of another conditional statement.
- Statement modifier
- A postfix conditional expression, i.e., a conditional expression (using for example if, unless or for) that is placed after the statement the executions of which it controls. It can also refer to a postfix looping expression.
- Return statement
- A statement that causes a function to end immediately and return to the caller.
- Recursion
- The process of calling the function that is currently executing.
- Base case
- A conditional branch in a recursive function that does not make a recursive call.
- Infinite recursion
- A recursion that doesn’t have a base case, or never reaches it. Eventually, an infinite recursion causes a runtime error, for which you may not want to wait because it may take a long time.
4.18 Exercises
- Write a subroutine that computes how many days, hours, minutes and seconds there are in the number of seconds passed as an argument to the subroutine.
- Write a script that computes how many days, hours, minutes and seconds there are in 240,000 seconds.
- Change your script to compute the number of days, hours, minutes and seconds there are in a number of seconds entered by the script user when prompted to give a number of seconds.
Solutions: Subsection ??.
Fermat’s Last Theorem says that there are no positive integers a, b, and c such that
| an + bn = cn |
for any values of n greater than 2.
- Write a function named
check-fermatthat takes four parameters—a, b, c, and n—and checks to see if Fermat’s theorem holds. If n is greater than 2 andan + bn = cn the program should print, “Holy smokes, Fermat was wrong!” Otherwise the program should print, “No, that doesn’t work.”
- Write a function that prompts the user to input values
for a, b, c, and n, converts them to
integers, and uses
check-fermatto check whether they violate Fermat’s theorem.
Solution: ??
If you are given three sticks, you may or may not be able to arrange them in a triangle. For example, if one of the sticks is 12 inches long and the other two are one inch long, you will not be able to get the short sticks to meet in the middle. For any three lengths, there is a simple test to see if it is possible to form a triangle:
If any of the three lengths is greater than the sum of the other two, then you cannot form a triangle. Otherwise, you can. (If the sum of two lengths equals the third, they form what is called a “degenerate” triangle.)
- Write a function named
is-trianglethat takes three positive numbers as arguments, and that prints either “Yes” or “No,” depending on whether you can form a triangle from sticks with the given lengths. - Write a function that prompts the user to input
three stick lengths and uses
is-triangleto check whether sticks with the given lengths can form a triangle.
Solution: ??
The Fibonacci numbers are a sequence of numbers such as:
| 1, 1, 2, 3, 5, 8, 13, 21, 34, … |
in which the first two numbers are equal to 1 and each subsequent number of the sequence is defined as the sum of the previous two (for example, 5 = 2 + 3, 8 = 3 + 5, etc.).
In mathematical notation, the Fibonacci numbers could be defined by recurrence as follows:
| F1 = 1, F2 = 1, and Fn = Fn−1 + Fn−2 |
- Write a program using a for loop that prints on screen the first 20 Fibonacci numbers.
- Write a program which prompts the user to enter a number n and, using a for loop, computes and displays the nth Fibonacci number.
Solution: ??
What is the output of the following program? Draw a stack diagram that shows the state of the program when it prints the result.
[fontshape=up]
sub recurse($n, $s) {
if ($n == 0) {
say $s;
} else {
recurse $n - 1, $n + $s;
}
}
recurse 3, 0;
- What would happen if you called the function like this: recurse(-1, 0)?
- Write a documentation comment (maybe in the form of a multiline comment) that explains everything someone would need to know in order to use this function (and nothing else).
Solution: ??
Are you using one of our books in a class?
We'd like to know about it. Please consider filling out this short survey.