Notice
This is an older HTML version of
New Version Available: For the best reading experience, please use our new HTML version which includes:
- Better accessibility compliance
- Responsive design for all devices
- Improved navigation and search
- Modern web standards
This older version is kept for reference but is no longer actively maintained.
Chapter 9 Immutable Objects
Java is an object-oriented language, which means that it uses objects to (1) represent data and (2) provide methods related to them. This way of organizing programs is a powerful design concept, and we will introduce it gradually throughout the remainder of the book.
An object is a collection of data that provides a set of methods.
For example, Scanner, which you saw in Section 3.2, is an object that provides methods for parsing input.
System.out and System.in are also objects.
Strings are objects, too.
They contain characters and provide methods for manipulating character data.
Other data types, like Integer, contain numbers and provide methods for manipulating number data.
We will explore some of these methods in this chapter.
9.1 Primitives vs Objects
Not everything in Java is an object: int, double, char, and boolean are primitive types.
When you declare a variable with a primitive type, Java reserves a small amount of memory to store its value.
Figure 9.1 shows how the following values are stored in memory:
| int number = -2; char symbol = '!'; |
As you learned in Section 7.2, an array variable stores a reference to an array.
For example, the following line declares a variable named array and creates an array of three characters:
| char[] array = {'c', 'a', 't'}; |
Figure 9.2 shows them both, with a box to represent the location of the variable and an arrow pointing to the location of the array.
Objects work in a similar way.
For example, this line declares a String variable named word and creates a String object, as shown in Figure 9.3:
| String word = "dog"; |
Objects and arrays are usually created with the new keyword, which allocates memory for them. For convenience, you don’t have to use new to create strings:
| String word1 = new String("dog"); // creates a string object String word2 = "dog"; // implicitly creates a string object |
Recall from Section 6.10 that you need to use the equals method to compare strings.
The equals method traverses the String objects and tests whether they contain the same characters.
To test whether two integers or other primitive types are equal, you can simply use the == operator.
But two String objects with the same characters would not be considered equal in the == sense.
The == operator, when applied to string variables, tests only whether they refer to the same object.
9.2 The null Keyword
Often when you declare an object variable, you assign it to reference an object. But sometimes you want to declare a variable that doesn’t refer to an object, at least initially.
In Java, the keyword null is a special value that means “no object”.
You can initialize object and array variables this way:
| String name = null; int[] combo = null; |
The value null is represented in memory diagrams by a small box with no arrow, as in Figure 9.4.
If you try to use a variable that is null by invoking a method or accessing an element, Java throws a NullPointerException:
| System.out.println(name.length()); // NullPointerException System.out.println(combo[0]); // NullPointerException |
On the other hand, it is perfectly fine to pass a null reference as an argument to a method, or to receive one as a return value.
In these situations, null is often used to represent a special condition or indicate an error.
9.3 Strings Are Immutable
If the Java library didn’t have a String class, we would have to use character arrays to store and manipulate text.
Operations like concatenation (+), indexOf, and substring would be difficult and inconvenient.
Fortunately, Java does have a String class that provides these and other methods.
For example, the methods toLowerCase and toUpperCase convert uppercase letters to lowercase, and vice versa.
These methods are often a source of confusion, because it sounds like they modify strings.
But neither these methods nor any others can change a string, because strings are immutable.
When you invoke toUpperCase on a string, you get a new String object as a result.
For example:
| String name = "Alan Turing"; String upperName = name.toUpperCase(); |
After these statements run, upperName refers to the string "ALAN TURING".
But name still refers to "Alan Turing".
A common mistake is to assume that toUpperCase somehow affects the original string:
| String name = "Alan Turing"; name.toUpperCase(); // ignores the return value System.out.println(name); |
The previous code displays "Alan Turing", because the value of name, which refers to the original String object, never changes.
If you want to change name to be uppercase, then you need to assign the return value:
| String name = "Alan Turing"; name = name.toUpperCase(); // references the new string System.out.println(name); |
A similar method is replace, which finds and replaces instances of one string within another.
This example replaces "Computer Science" with "CS":
| String text = "Computer Science is fun!"; text = text.replace("Computer Science", "CS"); |
As with toUpperCase, assigning the return value (to text) is important.
If you don’t assign the return value, invoking text.replace has no effect.
Strings are immutable by design, because it simplifies passing them as parameters and return values. And since the contents of a string can never change, two variables can reference the same string without one accidentally corrupting the other.
9.4 Wrapper Classes
Primitive types like int, double, and char cannot be null, and they do not provide methods.
For example, you can’t invoke equals on an int:
| int i = 5; System.out.println(i.equals(5)); // compiler error |
But for each primitive type, there is a corresponding wrapper class in the Java library.
The wrapper class for int is named Integer, with a capital I:
| Integer i = Integer.valueOf(5); System.out.println(i.equals(5)); // displays true |
Other wrapper classes include Boolean, Character, Double, and Long.
They are in the java.lang package, so you can use them without importing them.
Like strings, objects from wrapper classes are immutable, and you have to use the equals method to compare them:
| Integer x = Integer.valueOf(123); Integer y = Integer.valueOf(123); if (x == y) { // false System.out.println("x and y are the same object"); } if (x.equals(y)) { // true System.out.println("x and y have the same value"); } |
Because x and y refer to different objects, this code displays only “x and y have the same value”.
Each wrapper class defines the constants MIN_VALUE and MAX_VALUE.
For example, Integer.MIN_VALUE is -2147483648, and Integer.MAX_VALUE is 2147483647.
Because these constants are available in wrapper classes, you don’t have to remember them, and you don’t have to write them yourself.
Wrapper classes also provide methods for converting strings to and from primitive types.
For example, Integer.parseInt converts a string to an int.
In this context, parse means “read and translate”.
| String str = "12345"; int num = Integer.parseInt(str); |
Other wrapper classes provide similar methods, like Double.parseDouble and Boolean.parseBoolean.
They also provide toString, which returns a string representation of a value:
| int num = 12345; String str = Integer.toString(num); |
The result is the String object "12345".
It’s always possible to convert a primitive value to a string, but not the other way around. For example, say we try to parse an invalid string like this:
| String str = "five"; int num = Integer.parseInt(str); // NumberFormatException |
parseInt throws a NumberFormatException, because the characters in the string "five" are not digits.
9.5 Command-Line Arguments
Now that you know about strings, arrays, and wrapper classes, we can finally explain the args parameter of the main method, which we have been ignoring since Chapter 1.
If you are unfamiliar with the command-line interface, please read Appendix A.3.
Let’s write a program to find the maximum value in a sequence of numbers.
Rather than read the numbers from System.in by using a Scanner, we’ll pass them as command-line arguments.
Here is a starting point:
| import java.util.Arrays; public class Max { public static void main(String[] args) { System.out.println(Arrays.toString(args)); } } |
You can run this program from the command line by typing this:
| java Max |
The output indicates that args is an empty array; that is, it has no elements:
| [] |
If you provide additional values on the command line, they are passed as arguments to main.
For example, say you run the program like this:
| java Max 10 -3 55 0 14 |
The output is shown here:
| [10, -3, 55, 0, 14] |
It’s not clear from the output, but the elements of args are strings.
So args is the array {"10", "-3", "55", "0", "14"}.
To find the maximum number, we have to convert the arguments to integers.
The following code uses an enhanced for loop (see Section 7.8) to parse the arguments and find the largest value:
| int max = Integer.MIN_VALUE; for (String arg : args) { int value = Integer.parseInt(arg); if (value > max) { max = value; } } System.out.println("The max is " + max); |
We begin by initializing max to the smallest (most negative) number an int can represent.
That way, the first value we parse will replace max.
As we find larger values, they will replace max as well.
If args is empty, the result will be MIN_VALUE.
We can prevent this situation from happening by checking args at the beginning of the program:
| if (args.length == 0) { System.err.println("Usage: java Max <numbers>"); return; } |
It’s customary for programs that require command-line arguments to display a “usage” message if the arguments are not valid. For example, if you run javac or java from the command line without any arguments, you will get a very long message.
9.6 Argument Validation
As we discussed in Section 5.9, you should never assume that program input will be in the correct format. Sometimes users make mistakes, such as pressing the wrong key or misreading instructions.
Or even worse, someone might make intentional “mistakes” to see what your program will do. One way hackers break into computer systems is by entering malicious input that causes a program to fail.
Programmers can make mistakes too. It’s difficult to write bug-free software, especially when working in teams on large projects.
For all of these reasons, it’s good practice to validate arguments passed to methods, including the main method.
In the previous section, we did this by ensuring that args.length was not 0.
As a further example, consider a method that checks whether the first word of a sentence is capitalized.
We can write this method using the Character wrapper class:
| public static boolean isCapitalized(String str) { return Character.isUpperCase(str.charAt(0)); } |
The expression str.charAt(0) makes two assumptions: the string object referenced by str exists, and it has at least one character.
What if these assumptions don’t hold at run-time?
- If
strisnull, invokingcharAtwill cause aNullPointerException, because you can’t invoke a method onnull. - If
strrefers to an empty string, which is aStringobject with no characters,charAtwill cause aStringIndexOutOfBoundsException, because there is no character at index0.
We can prevent these exceptions by validating str at the start of the method.
If it’s invalid, we return before executing the rest of the method:
| public static boolean isCapitalized(String str) { if (str == null || str.isEmpty()) { return false; } return Character.isUpperCase(str.charAt(0)); } |
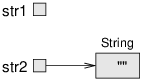
Notice that null and empty are different concepts, as shown in Figure 9.5.
The variable str1 is null, meaning that it doesn’t reference an object.
The variable str2 refers to the empty string, an object that exists.
Beginners sometimes make the mistake of checking for empty first.
Doing so causes a NullPointerException, because you can’t invoke methods on variables that are null:
| if (str.isEmpty() || str == null) { // wrong! |
Checking for null first prevents the NullPointerException.
If str is null, the || operator will short circuit (see Section 5.5) and evaluate to true immediately.
As a result, str.isEmpty() will not be called.
9.7 BigInteger Arithmetic
It might not be clear at this point why you would ever need an integer object when you can just use an int or long.
One advantage is the variety of methods that Integer and Long provide.
But there is another reason: when you need very large integers that exceed Long.MAX_VALUE.
BigInteger is a Java class that can represent arbitrarily large integers.
There is no upper bound except the limitations of memory size and processing speed.
Take a minute to read the documentation, which you can find by doing a web search for “Java BigInteger”.
To use BigIntegers, you have to import java.math.BigInteger at the beginning of your program.
There are several ways to create a BigInteger, but the simplest uses valueOf.
The following code converts a long to a BigInteger:
| long x = 17; BigInteger big = BigInteger.valueOf(x); |
You can also create BigIntegers from strings.
For example, here is a 20-digit integer that is too big to store using a long:
| String s = "12345678901234567890"; BigInteger bigger = new BigInteger(s); |
Notice the difference in the previous two examples: you use valueOf to convert integers, and new BigInteger to convert strings.
Since BigIntegers are not primitive types, the usual math operators don’t work.
Instead, we have to use methods like add.
To add two BigIntegers, we invoke add on one and pass the other as an argument:
| BigInteger a = BigInteger.valueOf(17); BigInteger b = BigInteger.valueOf(1700000000); BigInteger c = a.add(b); |
Like strings, BigInteger objects are immutable.
Methods like add, multiply, and pow all return new BigIntegers, rather than modify an existing one.
Internally, a BigInteger is implemented using an array of ints, similar to the way a string is implemented using an array of chars.
Each int in the array stores a portion of the BigInteger.
The methods of BigInteger traverse this array to perform addition, multiplication, etc.
For very long floating-point values, take a look at java.math.BigDecimal.
Interestingly, BigDecimal objects represent floating-point numbers internally by using a BigInteger!
9.8 Incremental Design
One challenge of programming, especially for beginners, is figuring out how to divide a program into methods. In this section, we present a design process that allows you to divide a program into methods as you go along. The process is called “encapsulation and generalization”. The essential steps are as follows:
-
Write a few lines of code in
mainor another method, and test them. - When they are working, wrap them in a new method and test again.
- If it’s appropriate, replace literal values with variables and parameters.
To demonstrate this process, we’ll develop methods that display multiplication tables. We begin by writing and testing a few lines of code. Here is a loop that displays the multiples of two, all on one line:
| for (int i = 1; i <= 6; i++) { System.out.printf("%4d", 2 * i); } System.out.println(); |
Each time through the loop, we display the value of 2 * i, padded with spaces so it’s four characters wide.
Since we use System.out.printf, the output appears on a single line.
After the loop, we call println to print a newline character.
Remember that in some environments, none of the output is displayed until the line is complete.
The output of the code so far is shown here:
| 2 4 6 8 10 12 |
The next step is to encapsulate the code; that is, we “wrap” the code in a method:
| public static void printRow() { for (int i = 1; i <= 6; i++) { System.out.printf("%4d", 2 * i); } System.out.println(); } |
Finally, we generalize the method to print multiples of other numbers by replacing the constant value 2 with a parameter n.
This step is called “generalization”, because it makes the method more general (less specific):
| public static void printRow(int n) { for (int i = 1; i <= 6; i++) { System.out.printf("%4d", n * i); // generalized n } System.out.println(); } |
Invoking this method with the argument 2 yields the same output as before.
With the argument 3, the output is as follows:
| 3 6 9 12 15 18 |
By now, you can probably guess how we are going to display a multiplication table: we’ll invoke printRow repeatedly with different arguments.
In fact, we’ll use another loop to iterate through the rows:
| for (int i = 1; i <= 6; i++) { printRow(i); } |
And the output looks like this:
| 1 2 3 4 5 6 2 4 6 8 10 12 3 6 9 12 15 18 4 8 12 16 20 24 5 10 15 20 25 30 6 12 18 24 30 36 |
9.9 More Generalization
The previous result is similar to the “nested loops” approach in Section 6.4.
However, the inner loop is now encapsulated in the printRow method.
We can encapsulate the outer loop in a method too:
| public static void printTable() { for (int i = 1; i <= 6; i++) { printRow(i); } } |
The initial version of printTable always displays six rows.
We can generalize it by replacing the literal 6 with a parameter:
| public static void printTable(int rows) { for (int i = 1; i <= rows; i++) { // generalized rows printRow(i); } } |
Here is the output of printTable(7):
| 1 2 3 4 5 6 2 4 6 8 10 12 3 6 9 12 15 18 4 8 12 16 20 24 5 10 15 20 25 30 6 12 18 24 30 36 7 14 21 28 35 42 |
That’s better, but it always displays the same number of columns.
We can generalize more by adding a parameter to printRow:
| public static void printRow(int n, int cols) { for (int i = 1; i <= cols; i++) { // generalized cols System.out.printf("%4d", n * i); } System.out.println(); } |
Now printRow takes two parameters: n is the value whose multiples should be displayed, and cols is the number of columns.
Since we added a parameter to printRow, we also have to change the line in printTable where it is invoked:
| public static void printTable(int rows) { for (int i = 1; i <= rows; i++) { printRow(i, rows); } } |
When this line executes, it evaluates rows and passes the value, which is 7 in this example, as an argument.
In printRow, this value is assigned to cols.
As a result, the number of columns equals the number of rows, so we get a square 7 x 7 table, instead of the previous 7 x 6 table.
When you generalize a method appropriately, you often find that it has capabilities you did not plan.
For example, you might notice that the multiplication table is symmetric.
Since ab = ba, all the entries in the table appear twice.
You could save ink by printing half of the table, and you would have to change only one line of printTable:
| printRow(i, i); // using i for both n and cols |
This means the length of each row is the same as its row number. The result is a triangular multiplication table:
| 1 2 4 3 6 9 4 8 12 16 5 10 15 20 25 6 12 18 24 30 36 7 14 21 28 35 42 49 |
Generalization makes code more versatile, more likely to be reused, and sometimes easier to write.
9.10 Vocabulary
- object-oriented:
- A way of organizing code and data into objects, rather than independent methods.
- object:
- A collection of related data that comes with a set of methods that operate on the data.
- primitive:
- A data type that stores a single value and provides no methods.
- immutable:
- An object that, once created, cannot be modified. Strings are immutable by design.
- wrapper class:
-
Classes in
java.langthat provide constants and methods for working with primitive types. - parse:
- In Chapter 2, we defined parse as what the compiler does to analyze a program. Now you know that it means to read a string and interpret or translate it.
- empty array:
- An array with no elements and a length of zero.
- design process:
- A process for determining what methods a class or program should have.
- encapsulate:
- To wrap data inside an object, or to wrap statements inside a method.
- generalize:
- To replace something unnecessarily specific (like a constant value) with something appropriately general (like a variable or parameter).
9.11 Exercises
The code for this chapter is in the ch09 directory of ThinkJavaCode2. See page ?? for instructions on how to download the repository. Before you start the exercises, we recommend that you compile and run the examples.
The point of this exercise is to explore Java types and fill in some of the details that aren’t covered in the chapter.
- Create a new program named Test.java and write a
mainmethod that contains expressions that combine various types using the+operator. For example, what happens when you “add” aStringand achar? Does it perform character addition or string concatenation? What is the type of the result? - Make a bigger copy of the following table and fill it in.
At the intersection of each pair of types, you should indicate whether it is legal to use the
+operator with these types, the operation that is performed (addition or concatenation), and the type of the result.boolean char int double String boolean char int double String - Think about some of the choices the designers of Java made, based on this table. How many of the entries seem unavoidable, as if there was no other choice? How many seem like arbitrary choices from several equally reasonable possibilities? Which entries seem most problematic?
- Here’s a puzzler: normally, the statement
x++is exactly equivalent tox = x + 1. But ifxis achar, it’s not exactly the same! In that case,x++is legal, butx = x + 1causes an error. Try it out. See what the error message is, and then see if you can figure out what is going on. - What happens when you add
""(the empty string) to the other types; for example,"" + 5?
You might be sick of the factorial method by now, but we’re going to do one more version.
- Create a new program called Big.java and write an iterative version of
factorial(using aforloop). - Display a table of the integers from 0 to 30 along with their factorials. At some point around 15, you will probably see that the answers are not correct anymore. Why not?
- Convert
factorialso that it performs its calculation using BigIntegers and returns aBigIntegeras a result. You can leave the parameter alone; it will still be an integer. - Try displaying the table again with your modified factorial method. Is it correct up to 30? How high can you make it go?
Many encryption algorithms depend on the ability to raise large integers to a power. Here is a method that implements an efficient algorithm for integer exponentiation:
| public static int pow(int x, int n) { if (n == 0) return 1; // find x to the n/2 recursively int t = pow(x, n / 2); // if n is even, the result is t squared // if n is odd, the result is t squared times x if (n % 2 == 0) { return t * t; } else { return t * t * x; } } |
The problem with this method is that it works only if the result is small enough to be represented by an int.
Rewrite it so that the result is a BigInteger.
The parameters should still be integers, though.
You should use the BigInteger methods add and multiply.
But don’t use BigInteger.pow; that would spoil the fun.
One way to calculate ex is to use the following infinite series expansion. The ith term in the series is xi / i!.
| ex = 1 + x + x2 / 2! + x3 / 3! + x4 / 4! + … |
- Write a method called
myexpthat takesxandnas parameters and estimates ex by adding the firstnterms of this series. You can use thefactorialmethod from Section 8.3 or your iterative version from the previous exercise. - You can make this method more efficient by observing that the numerator of each term is the same as its predecessor multiplied by
x, and the denominator is the same as its predecessor multiplied byi.Use this observation to eliminate the use of
Math.powandfactorial, and check that you get the same result. - Write a method called
checkthat takes a parameter,x, and displaysx,myexp(x), andMath.exp(x). The output should look like this:1.0 2.708333333333333 2.718281828459045 Use the escape sequence
'\t'to display a tab character between each of the values. - Vary the number of terms in the series (the second argument that
checksends tomyexp) and see the effect on the accuracy of the result. Adjust this value until the estimated value agrees with the correct answer whenxis 1. - Write a loop in
mainthat invokescheckwith the values 0.1, 1.0, 10.0, and 100.0. How does the accuracy of the result vary asxvaries? Compare the number of digits of agreement rather than the difference between the actual and estimated values. - Add a loop in
mainthat checksmyexpwith the values -0.1, -1.0, -10.0, and -100.0. Comment on the accuracy.
The goal of this exercise is to practice encapsulation and generalization using some of the examples in previous chapters.
- Starting with the code in Section 7.5, write a method called
powArraythat takes adoublearray,a, and returns a new array that contains the elements ofasquared. Generalize it to take a second argument and raise the elements ofato the given power. - Starting with the code in Section 7.8, write a method called
histogramthat takes anintarray of scores from 0 to (but not including) 100, and returns a histogram of 100 counters. Generalize it to take the number of counters as an argument.
The following code fragment traverses a string and checks whether it has the same number of opening and closing parentheses:
| String s = "((3 + 7) * 2)"; int count = 0; for (int i = 0; i < s.length(); i++) { char c = s.charAt(i); if (c == '(') { count++; } else if (c == ')') { count--; } } System.out.println(count); |
- Encapsulate this fragment in a method that takes a string argument and returns the final value of
count. - Test your method with multiple strings, including some that are balanced and some that are not.
- Generalize the code so that it works on any string. What could you do to generalize it more?