This HTML version of Think Complexity, 2nd Edition is provided for convenience, but it is not the best format of the book. In particular, some of the symbols are not rendered correctly.
You might prefer to read the PDF version.
Chapter 4 Scale-free networks
In this chapter, we’ll work with data from an online social network, and use a Watts-Strogatz graph to model it. The WS model has characteristics of a small world network, like the data, but it has low variability in the number of neighbors from node to node, unlike the data.
This discrepancy is the motivation for a network model developed by Barabási and Albert. The BA model captures the observed variability in the number of neighbors, and it has one of the small world properties, short path lengths, but it does not have the high clustering of a small world network.
The chapter ends with a discussion of WS and BA graphs as explanatory models for small world networks.
The code for this chapter is in chap04.ipynb in the respository for this book. More information about working with the code is in Section ??.
4.1 Social network data
Watts-Strogatz graphs are intended to model networks in the natural and social sciences. In their original paper, Watts and Strogatz looked at the network of film actors (connected if they have appeared in a movie together); the electrical power grid in the western United States; and the network of neurons in the brain of the roundworm C. elegans. They found that all of these networks had the high connectivity and low path lengths characteristic of small world graphs.
In this section we’ll perform the same analysis with a different dataset, a set of Facebook users and their friends. If you are not familiar with Facebook, users who are connected to each other are called “friends”, regardless of the nature of their relationship in the real world.
I’ll use data from the Stanford Network Analysis Project (SNAP), which shares large datasets from online social networks and other sources. Specifically, I’ll use their Facebook data1, which includes 4039 users and 88,234 friend relationships among them. This dataset is in the repository for this book, but it is also available from the SNAP website at http://thinkcomplex.com/snap.
The data file contains one line per edge, with users identified by integers from 0 to 4038. Here’s the code that reads the file:
| def read_graph(filename): G = nx.Graph() array = np.loadtxt(filename, dtype=int) G.add_edges_from(array) return G |
NumPy provides a function called loadtext that reads the
given file and returns the contents as a NumPy array. The
parameter dtype indicates that the “data type” of the array
is int.
Then we use add_edges_from to iterate the rows of the array
and make edges. Here are the results:
| >>> fb = read_graph('facebook_combined.txt.gz') >>> n = len(fb) >>> m = len(fb.edges()) >>> n, m (4039, 88234) |
The node and edge counts are consistent with the documentation of the dataset.
Now we can check whether this dataset has the characteristics of a small world graph: high clustering and low path lengths.
In Section ?? we wrote a function to compute
the network average clustering coefficient. NetworkX provides
a function called average_clustering, which does the same
thing a little faster.
But for larger graphs, they are both too slow, taking time proportional to n k2, where n is the number of nodes and k is the number of neighbors each node is connected to.
Fortunately, NetworkX provides a function that estimates the clustering coefficient by random sampling. You can invoke it like this:
| from networkx.algorithms.approximation import average_clustering average_clustering(G, trials=1000) |
The following function does something similar for path lengths.
| def sample_path_lengths(G, nodes=None, trials=1000): if nodes is None: nodes = list(G) else: nodes = list(nodes) pairs = np.random.choice(nodes, (trials, 2)) lengths = [nx.shortest_path_length(G, *pair) for pair in pairs] return lengths |
G is a graph, nodes is the list of nodes to sample
from, and trials is the number of random paths to sample.
If nodes is None, we sample from the entire graph.
pairs is a NumPy array of randomly chosen nodes with
one row for each trial and two columns.
The list comprehension enumerates the rows in the array and computes the shortest distance between each pair of nodes. The result is a list of path lengths.
estimate_path_length generates a list of random path lengths and
returns their mean:
| def estimate_path_length(G, nodes=None, trials=1000): return np.mean(sample_path_lengths(G, nodes, trials)) |
I’ll use average_clustering to compute C:
| C = average_clustering(fb) |
And estimate_path_lengths to compute L:
| L = estimate_path_lengths(fb) |
The clustering coefficient is about 0.61, which is high, as we expect if this network has the small world property.
And the average path is 3.7, which is quite short in a network of more than 4000 users. It’s a small world after all.
Now let’s see if we can construct a WS graph that has the same characteristics as this network.
4.2 WS Model
In the Facebook dataset, the average number of edges per node is about 22. Since each edge is connected to two nodes, the average degree is twice the number of edges per node:
| >>> k = int(round(2*m/n)) >>> k 44 |
We can make a WS graph with n=4039 and k=44. When p=0, we
get a ring lattice.
| lattice = nx.watts_strogatz_graph(n, k, 0) |
In this graph, clustering is high: C is 0.73, compared to 0.61
in the dataset. But L is 46, much higher
than in the dataset!
With p=1 we get a random graph:
| random_graph = nx.watts_strogatz_graph(n, k, 1) |
In the random graph, L is 2.6, even shorter than
in the dataset (3.7), but C is only 0.011, so that’s no good.
By trial and error, we find that when p=0.05 we get a WS graph with
high clustering and low path length:
| ws = nx.watts_strogatz_graph(n, k, 0.05, seed=15) |
In this graph C is 0.63, a bit higher than
in the dataset, and L is 3.2, a bit lower than in the dataset.
So this graph models the small world characteristics of the dataset
well.
So far, so good.
4.3 Degree
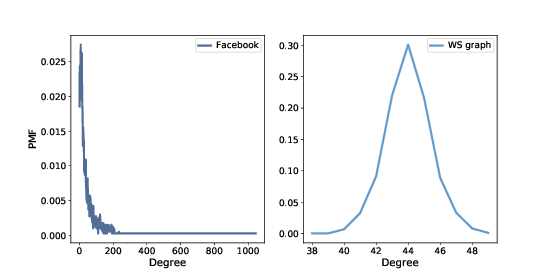
Figure 4.1: PMF of degree in the Facebook dataset and in the WS model.
If the WS graph is a good model for the Facebook network, it should have the same average degree across nodes, and ideally the same variance in degree.
This function returns a list of degrees in a graph, one for each node:
| def degrees(G): return [G.degree(u) for u in G] |
The mean degree in model is 44, which is close to the mean degree in the dataset, 43.7.
However, the standard deviation of degree in the model is 1.5, which is not close to the standard deviation in the dataset, 52.4. Oops.
What’s the problem? To get a better view, we have to look at the distribution of degrees, not just the mean and standard deviation.
I’ll represent the distribution of degrees with a Pmf object,
which is defined in the thinkstats2 module.
Pmf stands for “probability mass function”;
if you are not familiar with this concept,
you might want to read Chapter 3 of Think Stats, 2nd edition
at http://thinkcomplex.com/ts2.
Briefly, a Pmf maps from values to their probabilities.
A Pmf of degrees is a mapping from each possible degree, d, to the
fraction of nodes with degree d.
As an example, I’ll construct a graph with nodes 1, 2, and 3 connected to a central node, 0:
| G = nx.Graph() G.add_edge(1, 0) G.add_edge(2, 0) G.add_edge(3, 0) nx.draw(G) |
Here’s the list of degrees in this graph:
| >>> degrees(G) [3, 1, 1, 1] |
Node 0 has degree 3, the others have degree 1. Now I can make
a Pmf that represents this degree distribution:
| >>> from thinkstats2 import Pmf >>> Pmf(degrees(G)) Pmf({1: 0.75, 3: 0.25}) |
The result is a Pmf object that maps from each degree to a
fraction or probability. In this example, 75% of the nodes have
degree 1 and 25% have degree 3.
Now we can make a Pmf that contains node degrees from the
dataset, and compute the mean and standard deviation:
| >>> from thinkstats2 import Pmf >>> pmf_fb = Pmf(degrees(fb)) >>> pmf_fb.Mean(), pmf_fb.Std() (43.691, 52.414) |
And the same for the WS model:
| >>> pmf_ws = Pmf(degrees(ws)) >>> pmf_ws.mean(), pmf_ws.std() (44.000, 1.465) |
We can use the thinkplot module to plot the results:
| thinkplot.Pdf(pmf_fb, label='Facebook') thinkplot.Pdf(pmf_ws, label='WS graph') |
Figure ?? shows the two distributions. They are very different.
In the WS model, most users have about 44 friends; the minimum is 38 and the maximum is 50. That’s not much variation. In the dataset, there are many users with only 1 or 2 friends, but one has more than 1000!
Distributions like this, with many small values and a few very large values, are called heavy-tailed.
4.4 Heavy-tailed distributions
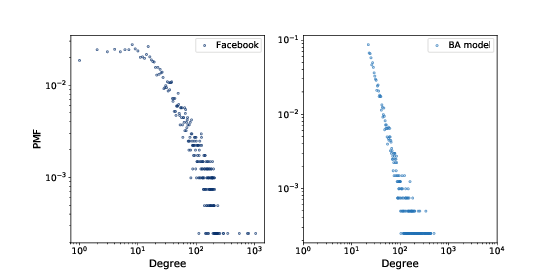
Figure 4.2: PMF of degree in the Facebook dataset and in the WS model, on a log-log scale.
Heavy-tailed distributions are a common feature in many areas of complexity science and they will be a recurring theme of this book.
We can get a clearer picture of a heavy-tailed distribution by plotting it on a log-log axis, as shown in Figure ??. This transformation emphasizes the tail of the distribution; that is, the probabilities of large values.
Under this transformation, the data fall approximately on a straight line, which suggests that there is a power law relationship between the largest values in the distribution and their probabilities. Mathematically, a distribution obeys a power law if
| PMF(k) ∼ k−α |
where PMF(k) is the fraction of nodes with degree k, α is a parameter, and the symbol ∼ indicates that the PMF is asymptotic to k−α as k increases.
If we take the log of both sides, we get
| logPMF(k) ∼ −α logk |
So if a distribution follows a power law and we plot PMF(k) versus k on a log-log scale, we expect a straight line with slope −α, at least for large values of k.
All power law distributions are heavy-tailed, but there are other heavy-tailed distributions that don’t follow a power law. We will see more examples soon.
But first, we have a problem: the WS model has the high clustering and low path length we see in the data, but the degree distribution doesn’t resemble the data at all. This discrepancy is the motivation for our next topic, the Barabási-Albert model.
4.5 Barabási-Albert model
In 1999 Barabási and Albert published a paper, “Emergence of Scaling in Random Networks”, that characterizes the structure of several real-world networks, including graphs that represent the interconnectivity of movie actors, web pages, and elements in the electrical power grid in the western United States. You can download the paper from http://thinkcomplex.com/barabasi.
They measure the degree of each node and compute PMF(k), the probability that a vertex has degree k. Then they plot PMF(k) versus k on a log-log scale. The plots fit a straight line, at least for large values of k, so Barabási and Albert conclude that these distributions are heavy-tailed.
They also propose a model that generates graphs with the same property. The essential features of the model, which distinguish it from the WS model, are:
- Growth:
- Instead of starting with a fixed number of vertices, the BA model starts with a small graph and adds vertices one at a time.
- Preferential attachment:
- When a new edge is created, it is more likely to connect to a vertex that already has a large number of edges. This “rich get richer” effect is characteristic of the growth patterns of some real-world networks.
Finally, they show that graphs generated by the Barabási-Albert (BA) model have a degree distribution that obeys a power law.
Graphs with this property are sometimes called scale-free networks, for reasons I won’t explain; if you are curious, you can read more at http://thinkcomplex.com/scale.
NetworkX provides a function that generates BA graphs. We will use it first; then I’ll show you how it works.
| ba = nx.barabasi_albert_graph(n=4039, k=22) |
The parameters are n, the number of nodes to generate, and
k, the number of edges each node starts with when it is added to
the graph. I chose k=22 because that is the average number
of edges per node in the dataset.
Figure 4.3: PMF of degree in the Facebook dataset and in the BA model, on a log-log scale.
The resulting graph has 4039 nodes and 21.9 edges per node. Since every edge is connected to two nodes, the average degree is 43.8, very close to the average degree in the dataset, 43.7.
And the standard deviation of degree is 40.9, which is a bit less than in the dataset, 52.4, but it is much better than what we got from the WS graph, 1.5.
Figure ?? shows the degree distributions for the
Facebook dataset and the BA model on a log-log scale. The model
is not perfect; in particular, it deviates from the data when
k is less than 10. But the tail looks like a straight line,
which suggests that this process generates degree distributions
that follow a power law.
So the BA model is better than the WS model at reproducing the degree distribution. But does it have the small world property?
In this example, the average path length, L, is 2.5, which is even more “small world” than the actual network, which has L=3.69. So that’s good, although maybe too good.
On the other hand, the clustering coefficient, C, is 0.037, not even close to the value in the dataset, 0.61. So that’s a problem.
Table ?? summarizes these results. The WS model captures the small world characteristics, but not the degree distribution. The BA model captures the degree distribution, at least approximately, and the average path length, but not the clustering coefficient.
In the exercises at the end of this chapter, you can explore other models intended to capture all of these characteristics.
4.6 Generating BA graphs
In the previous sections we used a NetworkX function to generate BA
graphs; now let’s see how it works. Here is a version
of barabasi_albert_graph, with some changes I made to
make it easier to read:
| def barabasi_albert_graph(n, k): G = nx.empty_graph(k) targets = list(range(k)) repeated_nodes = [] for source in range(k, n): G.add_edges_from(zip([source]*k, targets)) repeated_nodes.extend(targets) repeated_nodes.extend([source] * k) targets = _random_subset(repeated_nodes, k) return G |
The parameters are n, the number of nodes we want, and k, the
number of edges each new node gets (which will turn out to be
the average number of edges per node).
We start with a graph that has k nodes and no edges. Then we
initialize two variables:
targets:- The list of
knodes that will be connected to the next node. Initiallytargetscontains the originalknodes; later it will contain a random subset of nodes. repeated_nodes:- A list of existing nodes where each
node appears once for every edge it is connected to. When we
select from
repeated_nodes, the probability of selecting any node is proportional to the number of edges it has.
Each time through the loop, we add edges from the source to
each node in targets. Then we update repeated_nodes by
adding each target once and the new node k times.
Finally, we choose a subset of the nodes to be targets for the
next iteration. Here’s the definition of _random_subset:
| def _random_subset(repeated_nodes, k): targets = set() while len(targets) < k: x = random.choice(repeated_nodes) targets.add(x) return targets |
Each time through the loop, _random_subset chooses from
repeated_nodes and adds the chosen node to targets. Because
targets is a set, it automatically discards duplicates, so
the loop only exits when we have selected k different nodes.
4.7 Cumulative distributions
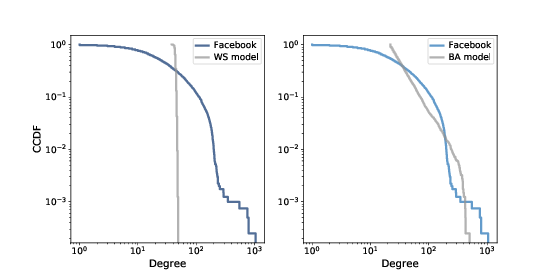
Figure 4.4: CDF of degree in the Facebook dataset along with the WS model (left) and the BA model (right), on a log-x scale.
Figure ?? represents the degree distribution by plotting the probability mass function (PMF) on a log-log scale. That’s how Barabási and Albert present their results and it is the representation used most often in articles about power law distributions. But it is not the best way to look at data like this.
A better alternative is a cumulative distribution function (CDF), which maps from a value, x, to the fraction of values less than or equal to x.
Given a Pmf, the simplest way to compute a cumulative probability
is to add up the probabilities for values up to and including x:
| def cumulative_prob(pmf, x): ps = [pmf[value] for value in pmf if value<=x] return np.sum(ps) |
For example, given the degree distribution in the dataset,
pmf_fb, we can compute the fraction of users with 25 or fewer
friends:
| >>> cumulative_prob(pmf_fb, 25) 0.506 |
The result is close to 0.5, which means that the median number of friends is about 25.
CDFs are better for visualization because they are less noisy than PMFs. Once you get used to interpreting CDFs, they provide a clearer picture of the shape of a distribution than PMFs.
The thinkstats module provides a class called Cdf that
represents a cumulative distribution function. We can use it
to compute the CDF of degree in the dataset.
| from thinkstats2 import Cdf cdf_fb = Cdf(degrees(fb), label='Facebook') |
And thinkplot provides a function called Cdf that plots
cumulative distribution functions.
| thinkplot.Cdf(cdf_fb) |
Figure ?? shows the degree CDF for the Facebook dataset along with the WS model (left) and the BA model (right). The x-axis is on a log scale.
Figure 4.5: Complementary CDF of degree in the Facebook dataset along with the WS model (left) and the BA model (right), on a log-log scale.
Clearly the CDF for the WS model is very different from the CDF from the data. The BA model is better, but still not very good, especially for small values.
In the tail of the distribution (values greater than 100) it looks like the BA model matches the dataset well enough, but it is hard to see. We can get a clearer view with one other view of the data: plotting the complementary CDF on a log-log scale.
The complementary CDF (CCDF) is defined
| CCDF(x) ≡ 1 − CDF(x) |
This definition is useful because if the PMF follows a power law, the CCDF also follows a power law:
| CCDF(x) ∼ | ⎛ ⎜ ⎜ ⎝ |
| ⎞ ⎟ ⎟ ⎠ |
|
where xm is the minimum possible value and α is a parameter that determines the shape of the distribution.
Taking the log of both sides yields:
| logCCDF(x) ∼ −α (logx − logxm) |
So if the distribution obeys a power law, we expect the CCDF on a log-log scale to be a straight line with slope −α.
Figure ?? shows the CCDF of degree for the Facebook data, along with the WS model (left) and the BA model (right), on a log-log scale.
With this way of looking at the data, we can see that the BA model matches the tail of the distribution (values above 20) reasonably well. The WS model does not.
4.8 Explanatory models
We started the discussion of networks with Milgram’s Small World Experiment, which shows that path lengths in social networks are surprisingly small; hence, “six degrees of separation”.
When we see something surprising, it is natural to ask “Why?” but sometimes it’s not clear what kind of answer we are looking for. One kind of answer is an explanatory model (see Figure ??). The logical structure of an explanatory model is:
- In a system, S, we see something observable, O, that warrants explanation.
- We construct a model, M, that is analogous to the system; that is, there is a correspondence between the elements of the model and the elements of the system.
- By simulation or mathematical derivation, we show that the model exhibits a behavior, B, that is analogous to O.
- We conclude that S exhibits O because S is similar to M, M exhibits B, and B is similar to O.
At its core, this is an argument by analogy, which says that if two things are similar in some ways, they are likely to be similar in other ways.
Argument by analogy can be useful, and explanatory models can be satisfying, but they do not constitute a proof in the mathematical sense of the word.
Remember that all models leave out, or “abstract away”, details that we think are unimportant. For any system there are many possible models that include or ignore different features. And there might be models that exhibit different behaviors that are similar to O in different ways. In that case, which model explains O?
The small world phenomenon is an example: the Watts-Strogatz (WS) model and the Barabási-Albert (BA) model both exhibit elements of small world behavior, but they offer different explanations:
- The WS model suggests that social networks are “small” because they include both strongly-connected clusters and “weak ties” that connect clusters (see http://thinkcomplex.com/weak).
- The BA model suggests that social networks are small because they include nodes with high degree that act as hubs, and that hubs grow, over time, due to preferential attachment.
As is often the case in young areas of science, the problem is not that we have no explanations, but too many.
4.9 Exercises
In Section ?? we discussed two explanations for the small world phenomenon, “weak ties” and “hubs”. Are these explanations compatible; that is, can they both be right? Which do you find more satisfying as an explanation, and why?
Is there data you could collect, or experiments you could perform, that would provide evidence in favor of one model over the other?
Choosing among competing models is the topic of Thomas Kuhn’s essay, “Objectivity, Value Judgment, and Theory Choice”, which you can read at http://thinkcomplex.com/kuhn.
What criteria does Kuhn propose for choosing among competing models? Do these criteria influence your opinion about the WS and BA models? Are there other criteria you think should be considered?
NetworkX provides a function called powerlaw_cluster_graph that
implements the "Holme and Kim algorithm for growing graphs with
powerlaw degree distribution and approximate average clustering".
Read the documentation of this function (http://thinkcomplex.com/hk) and see if you can use it to
generate a graph that has the same number of nodes as the Facebook
dataset, the same average degree, and the same clustering coefficient.
How does the degree distribution in the model compare to the actual
distribution?
Data files from the Barabási and Albert paper are available from
http://thinkcomplex.com/netdata. Their actor collaboration data is included in the repository for this book in a
file named actor.dat.gz. The following function reads the file and
builds the graph.
| import gzip def read_actor_network(filename, n=None): G = nx.Graph() with gzip.open(filename) as f: for i, line in enumerate(f): nodes = [int(x) for x in line.split()] G.add_edges_from(thinkcomplexity.all_pairs(nodes)) if n and i >= n: break return G |
Compute the number of actors in the graph and the average degree. Plot the PMF of degree on a log-log scale. Also plot the CDF of degree on a log-x scale, to see the general shape of the distribution, and on a log-log scale, to see whether the tail follows a power law.
Note: The actor network is not connected, so you might want to use
nx.connected_component_subgraphs to find connected subsets of the
nodes.
- 1
- J. McAuley and J. Leskovec. Learning to Discover Social Circles in Ego Networks. NIPS, 2012.
Contribute
If you would like to make a contribution to support my books, you can use the button below and pay with PayPal. Thank you!
Are you using one of our books in a class?
We'd like to know about it. Please consider filling out this short survey.