Chapter 14  Case study: The Volunteer’s Dilemma

Molly Grossman, Mandy Korpusik, and Philip Loh

14.1  The prairie dog’s dilemma

Suppose you are a prairie dog assigned to guard duty with other prairie dogs from your town. When you see a predator coming, you have two choices: sound the alarm or remain silent. If you sound the alarm, you help ensure the safety of the other prairie dogs, but you also encourage the predator to come after you. For you, it is safer to remain silent, but if all guards remain silent, everyone is less safe, including you. What should you do when you see a predator?

This scenario is an example of the Volunteer’s Dilemma, a game similar to the Prisoner’s Dilemma discussed in Section 10.5. In the Prisoner’s Dilemma each player has two options—cooperate and defect. In the Volunteer’s Dilemma each player also has two options—volunteer (sound the alarm in our prairie dog example) or ignore (remain silent). If one player volunteers then the other player is better off ignoring. But if both players ignore, both pay a high cost.

In the Prisoner’s Dilemma, both players are better off if they both cooperate; however, since neither knows what the other will do, each independently comes to the conclusion that he or she should defect.

In the Volunteer’s Dilemma, it is not immediately clear what outcome is best for both players. Suppose the players are named Alice and Bob. If Alice volunteers, Bob is better off ignoring; if Alice ignores, Bob is better off volunteering. This does not provide a clear best strategy for Bob. By the same analysis, Alice reaches the same conclusion: if Bob volunteers, she is better off ignoring; and if Bob ignores, she is better off volunteering.

Instead of one optimal outcome, as in the Prisoner’s Dilemma, there are two equally good outcomes: Bob volunteers and Alice ignores, or Bob ignores and Alice volunteers.

In the prairie dog town, there are more than two guards. As in the scenario with just Alice and Bob, only one player needs to volunteer to benefit the entire town. So there are as many good outcomes as guards—in each case, one guard volunteers and the others ignore.

If one guard is always going to volunteer, though, then there is little point in having multiple guards. To make the situation more fair, we can allow the guards to distribute the burden of volunteering among themselves by making decisions randomly. That is, each guard chooses to ignore with some probability γ or to volunteer with probability 1 − γ. The optimal value for γ is that where each player volunteers as little as necessary to produce the common good.

14.2  Analysis

Marco Archetti investigates the optimal value of γ in his paper “The Volunteer’s Dilemma and the Optimal Size of a Social Group.” This section replicates his analysis.

When each player volunteers with the optimal probability, the expected payoff of volunteering is the same as the expected payoff of ignoring. Were the payoff of volunteering higher than the payoff of ignoring, the player would volunteer more often and ignore less; the opposite is true were the payoff of ignoring higher than the payoff of volunteering.

The optimal probability depends on the costs and benefits of each option. In fact, the optimal γ for two individuals is

where c is the cost of volunteering, and a is the total cost if nobody volunteers. In the prairie dog example, where the damage of nobody volunteering is high, γ₂ is small.

If you transfer more prairie dogs to guard duty, there are more players to share the cost of volunteering, so we expect the probability of each player ignoring should increase. Indeed, Archetti shows:

γ_N increases with N, so as the number of players increases, each player volunteers less.

But, surprisingly, adding more guards does not make the town safer. If everyone volunteers at the optimal probability, the probability that everyone except you ignores is γ_N^N−1, which is γ₂, so it doesn’t depend on N. If you also ignore with probability γ_N, the probability that everyone ignores is γ₂ γ_N, which increases with N.

This result is disheartening. We can ensure that the high-damage situation never occurs by placing the entire burden of the common good on one individual who must volunteer all the time. We could instead be more fair and distribute the burden of volunteering among the players by asking each of them to volunteer some percentage of the time, but the high-damage situation will occur more frequently as the number of players who share the burden increases.

14.3  The Norms Game

At some colleges, cheating is commonplace and students seldom report cheaters. At other colleges, cheating is rare and likely to be reported and punished. The explicit and implicit rules about cheating, and reporting cheaters, are social norms.

Social norms influence the behavior of individuals: for example, you might be more likely to cheat if you think it is common and seldom punished. But individuals also influence social norms: if more people report cheaters, fewer people will cheat. We can extend the analysis from the previous section to model these effects.

Our model is based on a genetic algorithm presented by Robert Axelrod in “Promoting Norms: An Evolutionary Approach to Norms.” Genetic algorithms model the process of natural evolution. We create a population of simulated individuals with different attributes. The individuals interact in ways that test their fitness (by some definition of “fitness”). Individuals with higher fitness are more likely to reproduce, so over time the average fitness of the population increases.

In the cheating scenario, the relevant attributes are:

boldness

: the likelihood that an individual cheats, and

vengefulness

: the likelihood that an individual reports a cheater.

The players interact by playing two games, called “cheat-or-not” and “punish-or-not.” In the first, each player decides whether to cheat, depending on the value of boldness. In the second, each player decides whether to report a cheater, depending on vengefulness. These subgames are played several times per generation so each player has several opportunities to cheat and punish cheaters.

The fitness of each player depends on how they play the subgames. When a player cheats, his fitness increases by reward points, but the fitness of others decreases by damage points. Each individual who reports a cheater loses cost fitness points and causes the cheater to lose punishment fitness points.

At the end of each generation, individuals with the highest fitness levels have the most children in the next generation. The properties of each individual in the new generation are then mutated to maintain variation.

This code summarizes the structure of the simulation:

for generations in range(many):
    for steps in range(repetitions):
        for person in persons:
            cheat_or_not()
            punish_or_not()
    genetic_repopulation()
    genetic_mutation()

14.4  Results

---

Figure 14.1: End conditions after 300 generations.

---

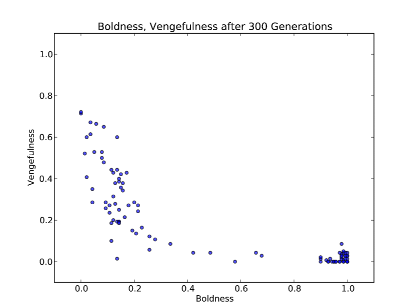
Each run starts with a random population and runs for 300 generations. The parameters of the simulation are reward = 3, damage = 1, cost = 2, punishment = 9. At the end, we compute the mean boldness and vengefulness of the population. Figure 14.1 shows the results; each dot represents one run of the simulation.

There are two clear clusters, one with low boldness and one with high boldness. When boldness is low, the average vengefulness is spread out, which suggests that vengefulness does not matter very much. If few people cheat, opportunities to punish are rare and the effect of vengefulness on fitness is small. When boldness is high, vengefulness is consistently low.

In the low-boldness cluster, average fitness is higher, so individuals in the high-boldness cluster would be better off if they could move. But if they make a unilateral move toward higher boldness or higher vengefulness, their fitness suffers. So the high-boldness scenario is stable, which is why this cluster exists.

14.5  Improving the chances

---

Figure 14.2: Proportion of good outcomes, varying the cost of reporting cheaters and the punishment for cheating.

---

Suppose you are founding a new college and thinking about the academic culture you want to create. You probably prefer an environment where cheating is rare. But our simulations suggest that there are two stable outcomes, with low and high rates of cheating. What can you do to improve the chances of reaching (and staying in) the low-cheating regime?

The parameters of the simulation affect the probability of the outcomes. In the previous section, the parameters were reward = 3, damage = 1, cost = 2, punishment = 9. The probability of reaching the low-cheating regime was about 50%. If you were founding a new college, you might not like those odds.

The parameters that have the strongest effect on the outcome are cost, the cost of reporting a cheater, and punishment, the cost of getting caught. Figure 14.2 shows how the proportion of good outcomes depends on these parameters.

There are two ways to increase the chances of a good outcome, decreasing cost or increasing punishment. If we fix punishment=9 and decrease cost to 1, the probability of a good outcome is 80%. If we fix cost=2, to achieve the same probability, we have to increase punishment to 11.

Which option is more appealing depends on practical and cultural considerations. Of course, we have to be careful not to take this model too seriously. It is a highly abstracted model of complex human behavior. Nevertheless, it provides insight into the emergence and stability of social norms.

Like this book?

Are you using one of our books in a class?

Think Bayes

Think Python

Think Stats

Think Complexity